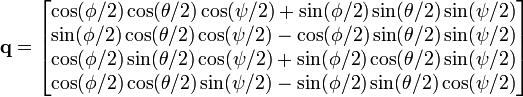|
Quaternion(四元数)和旋转
本文介绍了四元数以及如何在OpenGL中使用四元数表示旋转。
|
Quaternion 的定义四元数一般定义如下: q=w+xi+yj+zk 其中 w,x,y,z是实数。同时,有: i*i=-1
j*j=-1
k*k=-1
四元数也可以表示为: q=[w,v] 其中v=(x,y,z)是矢量,w是标量,虽然v是矢量,但不能简单的理解为3D空间的矢量,它是4维空间中的的矢量,也是非常不容易想像的。 通俗的讲,一个四元数(Quaternion)描述了一个旋转轴和一个旋转角度。这个旋转轴和这个角度可以通过 Quaternion::ToAngleAxis转换得到。当然也可以随意指定一个角度一个旋转轴来构造一个Quaternion。这个角度是相对于单位四元数而言的,也可以说是相对于物体的初始方向而言的。 当用一个四元数乘以一个向量时,实际上就是让该向量围绕着这个四元数所描述的旋转轴,转动这个四元数所描述的角度而得到的向量。 四元组的优点1有多种方式可表示旋转,如 axis/angle、欧拉角(Euler angles)、矩阵(matrix)、四元组等。 相对于其它方法,四元组有其本身的优点:
Quaternion 的基本运算1Normalizing a quaternion// normalising a quaternion works similar to a vector. This method will not do anything
// if the quaternion is close enough to being unit-length. define TOLERANCE as something
// small like 0.00001f to get accurate results
void Quaternion::normalise()
{
// Don't normalize if we don't have to
float mag2 = w * w + x * x + y * y + z * z;
if ( mag2!=0.f && (fabs(mag2 - 1.0f) > TOLERANCE)) {
float mag = sqrt(mag2);
w /= mag;
x /= mag;
y /= mag;
z /= mag;
}
}
The complex conjugate of a quaternion// We need to get the inverse of a quaternion to properly apply a quaternion-rotation to a vector
// The conjugate of a quaternion is the same as the inverse, as long as the quaternion is unit-length
Quaternion Quaternion::getConjugate()
{
return Quaternion(-x, -y, -z, w);
}
Multiplying quaternions// Multiplying q1 with q2 applies the rotation q2 to q1
Quaternion Quaternion::operator* (const Quaternion &rq) const
{
// the constructor takes its arguments as (x, y, z, w)
return Quaternion(w * rq.x + x * rq.w + y * rq.z - z * rq.y,
w * rq.y + y * rq.w + z * rq.x - x * rq.z,
w * rq.z + z * rq.w + x * rq.y - y * rq.x,
w * rq.w - x * rq.x - y * rq.y - z * rq.z);
}
Rotating vectors// Multiplying a quaternion q with a vector v applies the q-rotation to v
Vector3 Quaternion::operator* (const Vector3 &vec) const
{
Vector3 vn(vec);
vn.normalise();
Quaternion vecQuat, resQuat;
vecQuat.x = vn.x;
vecQuat.y = vn.y;
vecQuat.z = vn.z;
vecQuat.w = 0.0f;
resQuat = vecQuat * getConjugate();
resQuat = *this * resQuat;
return (Vector3(resQuat.x, resQuat.y, resQuat.z));
}
How to convert to/from quaternions1Quaternion from axis-angle// Convert from Axis Angle
void Quaternion::FromAxis(const Vector3 &v, float angle)
{
float sinAngle;
angle *= 0.5f;
Vector3 vn(v);
vn.normalise();
sinAngle = sin(angle);
x = (vn.x * sinAngle);
y = (vn.y * sinAngle);
z = (vn.z * sinAngle);
w = cos(angle);
}
Quaternion from Euler angles// Convert from Euler Angles
void Quaternion::FromEuler(float pitch, float yaw, float roll)
{
// Basically we create 3 Quaternions, one for pitch, one for yaw, one for roll
// and multiply those together.
// the calculation below does the same, just shorter
float p = pitch * PIOVER180 / 2.0;
float y = yaw * PIOVER180 / 2.0;
float r = roll * PIOVER180 / 2.0;
float sinp = sin(p);
float siny = sin(y);
float sinr = sin(r);
float cosp = cos(p);
float cosy = cos(y);
float cosr = cos(r);
this->x = sinr * cosp * cosy - cosr * sinp * siny;
this->y = cosr * sinp * cosy + sinr * cosp * siny;
this->z = cosr * cosp * siny - sinr * sinp * cosy;
this->w = cosr * cosp * cosy + sinr * sinp * siny;
normalise();
}
Quaternion to Matrix// Convert to Matrix
Matrix4 Quaternion::getMatrix() const
{
float x2 = x * x;
float y2 = y * y;
float z2 = z * z;
float xy = x * y;
float xz = x * z;
float yz = y * z;
float wx = w * x;
float wy = w * y;
float wz = w * z;
// This calculation would be a lot more complicated for non-unit length quaternions
// Note: The constructor of Matrix4 expects the Matrix in column-major format like expected by
// OpenGL
return Matrix4( 1.0f - 2.0f * (y2 + z2), 2.0f * (xy - wz), 2.0f * (xz + wy), 0.0f,
2.0f * (xy + wz), 1.0f - 2.0f * (x2 + z2), 2.0f * (yz - wx), 0.0f,
2.0f * (xz - wy), 2.0f * (yz + wx), 1.0f - 2.0f * (x2 + y2), 0.0f,
0.0f, 0.0f, 0.0f, 1.0f)
}
Quaternion to axis-angle// Convert to Axis/Angles
void Quaternion::getAxisAngle(Vector3 *axis, float *angle)
{
float scale = sqrt(x * x + y * y + z * z);
axis->x = x / scale;
axis->y = y / scale;
axis->z = z / scale;
*angle = acos(w) * 2.0f;
}
Quaternion 插值2线性插值最简单的插值算法就是线性插值,公式如: q(t)=(1-t)q1 + t q2 但这个结果是需要规格化的,否则q(t)的单位长度会发生变化,所以 q(t)=(1-t)q1+t q2 / || (1-t)q1+t q2 || 球形线性插值尽管线性插值很有效,但不能以恒定的速率描述q1到q2之间的曲线,这也是其弊端,我们需要找到一种插值方法使得q1->q(t)之间的夹角θ是线性的,即θ(t)=(1-t)θ1+t*θ2,这样我们得到了球形线性插值函数q(t),如下: q(t)=q1 * sinθ(1-t)/sinθ + q2 * sinθt/sineθ 如果使用D3D,可以直接使用 D3DXQuaternionSlerp 函数就可以完成这个插值过程。 用 Quaternion 实现 Camera 旋转总体来讲,Camera 的操作可分为如下几类:
下面是一个使用了 Quaternion 的 Camera 类: class Camera {
private:
Quaternion m_orientation;
public:
void rotate (const Quaternion& q);
void rotate(const Vector3& axis, const Radian& angle);
void roll (const GLfloat angle);
void yaw (const GLfloat angle);
void pitch (const GLfloat angle);
};
void Camera::rotate(const Quaternion& q)
{
// Note the order of the mult, i.e. q comes after
m_Orientation = q * m_Orientation;
}
void Camera::rotate(const Vector3& axis, const Radian& angle)
{
Quaternion q;
q.FromAngleAxis(angle,axis);
rotate(q);
}
void Camera::roll (const GLfloat angle) //in radian
{
Vector3 zAxis = m_Orientation * Vector3::UNIT_Z;
rotate(zAxis, angleInRadian);
}
void Camera::yaw (const GLfloat angle) //in degree
{
Vector3 yAxis;
{
// Rotate around local Y axis
yAxis = m_Orientation * Vector3::UNIT_Y;
}
rotate(yAxis, angleInRadian);
}
void Camera::pitch (const GLfloat angle) //in radian
{
Vector3 xAxis = m_Orientation * Vector3::UNIT_X;
rotate(xAxis, angleInRadian);
}
void Camera::gluLookAt() {
GLfloat m[4][4];
identf(&m[0][0]);
m_Orientation.createMatrix (&m[0][0]);
glMultMatrixf(&m[0][0]);
glTranslatef(-m_eyex, -m_eyey, -m_eyez);
}
用 Quaternion 实现 trackball用鼠标拖动物体在三维空间里旋转,一般设计一个 trackball,其内部实现也常用四元数。 class TrackBall
{
public:
TrackBall();
void push(const QPointF& p);
void move(const QPointF& p);
void release(const QPointF& p);
QQuaternion rotation() const;
private:
QQuaternion m_rotation;
QVector3D m_axis;
float m_angularVelocity;
QPointF m_lastPos;
};
void TrackBall::move(const QPointF& p)
{
if (!m_pressed)
return;
QVector3D lastPos3D = QVector3D(m_lastPos.x(), m_lastPos.y(), 0.0f);
float sqrZ = 1 - QVector3D::dotProduct(lastPos3D, lastPos3D);
if (sqrZ > 0)
lastPos3D.setZ(sqrt(sqrZ));
else
lastPos3D.normalize();
QVector3D currentPos3D = QVector3D(p.x(), p.y(), 0.0f);
sqrZ = 1 - QVector3D::dotProduct(currentPos3D, currentPos3D);
if (sqrZ > 0)
currentPos3D.setZ(sqrt(sqrZ));
else
currentPos3D.normalize();
m_axis = QVector3D::crossProduct(lastPos3D, currentPos3D);
float angle = 180 / PI * asin(sqrt(QVector3D::dotProduct(m_axis, m_axis)));
m_axis.normalize();
m_rotation = QQuaternion::fromAxisAndAngle(m_axis, angle) * m_rotation;
m_lastPos = p;
}
Yaw, pitch, roll 的含义3Yaw – Vertical axis:
Pitch – Lateral axis
Roll – Longitudinal axis
The Position of All three axes
|
四元数与欧拉角之间的转换
在3D图形学中,最常用的旋转表示方法便是四元数和欧拉角,比起矩阵来具有节省存储空间和方便插值的优点。本文主要归纳了两种表达方式的转换,计算公式采用3D笛卡尔坐标系:
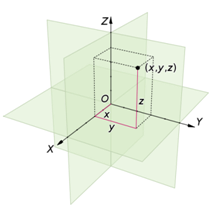
图1 3D Cartesian coordinate System (from wikipedia)
定义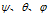 分别为绕Z轴、Y轴、X轴的旋转角度,如果用Tait-Bryan angle表示,分别为Yaw、Pitch、Roll。
分别为绕Z轴、Y轴、X轴的旋转角度,如果用Tait-Bryan angle表示,分别为Yaw、Pitch、Roll。
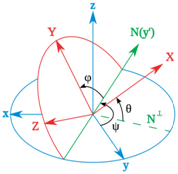
图2 Tait-Bryan angles (from wikipedia)
一、四元数的定义
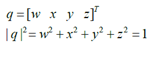
通过旋转轴和绕该轴旋转的角度可以构造一个四元数:
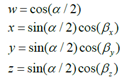
其中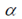 是绕旋转轴旋转的角度,
是绕旋转轴旋转的角度,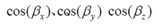 为旋转轴在x,y,z方向的分量(由此确定了旋转轴)。
为旋转轴在x,y,z方向的分量(由此确定了旋转轴)。
二、欧拉角到四元数的转换
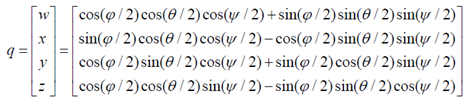
三、四元数到欧拉角的转换

arctan和arcsin的结果是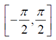 ,这并不能覆盖所有朝向(对于
,这并不能覆盖所有朝向(对于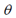 角
角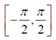 的取值范围已经满足),因此需要用atan2来代替arctan。
的取值范围已经满足),因此需要用atan2来代替arctan。
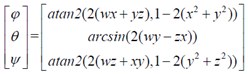
四、在其他坐标系下使用
在其他坐标系下,需根据坐标轴的定义,调整一下以上公式。如在Direct3D中,笛卡尔坐标系的X轴变为Z轴,Y轴变为X轴,Z轴变为Y轴(无需考虑方向)。
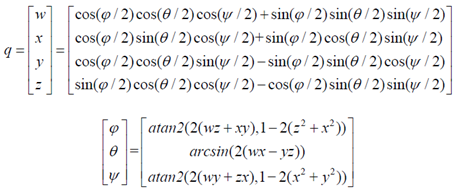
五、示例代码
http://www.cppblog.com/Files/heath/Euler2Quaternion.rar
Demo渲染两个模型,左边使用欧拉角,右边使用四元数,方向键Up、Left、Right旋转模型。
Spatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of “quaternions” was first presented by Euler some seventy years earlier than Hamilton to solve the problem of magic squares. For this reason the dynamics community commonly refers to quaternions in this application as “Euler parameters”.
Contents[hide] |
[edit] Definition
A unit quaternion can be described as:
We can associate a quaternion with a rotation around an axis by the following expression
where α is a simple rotation angle (the value in radians of the angle of rotation) and cos(βx), cos(βy) and cos(βz) are the “direction cosines” locating the axis of rotation (Euler’s Theorem).
[edit] Rotation matrices
The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/left-handed rotation by the unit quaternion 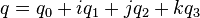 is given by the inhomogeneous expression
is given by the inhomogeneous expression
or equivalently, by the homogeneous expression
If  is not a unit quaternion then the homogeneous form is still a scalar multiple of a rotation matrix, while the inhomogeneous form is in general no longer an orthogonal matrix. This is why in numerical work the homogeneous form is to be preferred if distortion is to be avoided.
is not a unit quaternion then the homogeneous form is still a scalar multiple of a rotation matrix, while the inhomogeneous form is in general no longer an orthogonal matrix. This is why in numerical work the homogeneous form is to be preferred if distortion is to be avoided.
The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/left-handed rotation with Euler angles φ, θ, ψ, with x-y-z convention, is given by:
[edit] Conversion
By combining the quaternion representations of the Euler rotations we get
For Euler angles we get:
arctan and arcsin have a result between −π/2 and π/2. With three rotations between −π/2 and π/2 you can’t have all possible orientations. You need to replace the arctan by atan2 to generate all the orientations.
[edit] Relationship with Tait–Bryan angles
Similarly for Euler angles, we use the Tait–Bryan angles (in terms of flight dynamics):
- Roll –
 : rotation about the X-axis
: rotation about the X-axis
- Pitch –
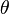 : rotation about the Y-axis
: rotation about the Y-axis
- Yaw –
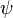 : rotation about the Z-axis
: rotation about the Z-axis
where the X-axis points forward, Y-axis to the right and Z-axis downward and in the example to follow the rotation occurs in the order yaw, pitch, roll (about body-fixed axes).
[edit] Singularities
One must be aware of singularities in the Euler angle parametrization when the pitch approaches ±90° (north/south pole). These cases must be handled specially. The common name for this situation is gimbal lock.
Code to handle the singularities is derived on this site: www.euclideanspace.com
[edit] See also
- Rotation operator (vector space)
- Quaternions and spatial rotation
- Euler Angles
- Rotation matrix
- Rotation formalisms in three dimensions
[edit] External links
- Q60. How do I convert Euler rotation angles to a quaternion? and related questions at The Matrix and Quaternions FAQ
- 本文固定链接: http://www.wy182000.com/2012/07/17/quaternion四元数和旋转以及yaw-pitch-roll-的含义/
- 转载请注明: wy182000 于 Studio 发表






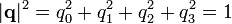







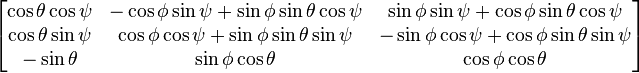
![\mathbf{q} = R_z(\psi)R_y(\theta)R_x(\phi) = [\cos (\psi /2) + \mathbf{k}\sin (\psi /2)][\cos (\theta /2) + \mathbf{j}\sin (\theta /2)][\cos (\phi /2) + \mathbf{i}\sin (\phi /2)]](http://upload.wikimedia.org/wikipedia/en/math/b/b/9/bb904981a020685900d9320e9b41f09b.png)